Mandelbulb 3D Tutorial: Colour and Lighting cont.

Next, the Ambient tab:

I've played around with each little slide and button for half an hour and still, can't seem to come up with good explanations for all of them. I blame this on a lack of coffee. But I'll try my best and I'm sure through trying yourself, you'll get the general idea:

The "Amb" colours and slider affect the colour and intensity of the all other colours. They're like coloured lenses through which you're looking at your image, and the slide adjusts their brightness. Sliding all the way to the left essentially turns them off.

The Depth colours and slider affects the ambient background colours. The background gradients from your one chosen colour into the other.

Then you have the fog slide :) Adds spookiness to your image :) ... I remember using it in my very first 3D fractal art, back when I had no idea what I was doing. Simply adds luminescent fog of the colour of your choice around your fractal.

The fog offset decreases or increases general fogginess to the picture.
Far offset does a similar thing but starts from far back behind the fractal.

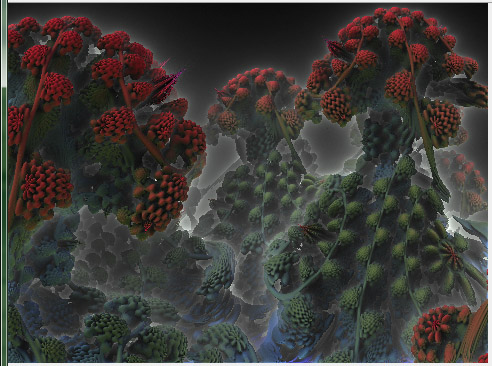
The Ambient Shadow bar is a strange one... From my observations using my forest image below, its was like I was turning a light deep within the fractal on and off, making the fractal glow or go completely dead. Again, I'm probably not quite understanding this properly yet and will add more info here once I've had more experience.

My apologies for such vague descriptions but I am truly a beginner myself. Just play around with them like I've been doing and you'll understand what they do intuitively. Here's my image after some tinkering. (Note that though I didn't (and still don't) really understand how most of the Ambient settings work, I still created this from a pre-conceived idea in my head. My forest, but foggy in the night time):

Mandelbulb Dark Forest

Mandelbulb 3D Tutorial: Lighting and Colouring

To continue...! Once again, let me state that I've only just started with Mandelbulb 3D and thus my knowledge is still in it's nascent stage. I'm doing this tutorial at this stage deliberately, so that all you guys who need it feel that I'm on more or less the same level as you: I know nothing to nearly nothing :P

Ok, on we go. To start, you need to open up your .m3i or .m3p that you saved last time (see previous tutorial page).
If opening an .m3p, remember to click on "Calculate 3D" to render your image once again.

If you remember, this is the image I am working with:

Now you need to go to the Lighting window, which should have opened up when you opened Mandelbulb 3D:

There it is. The first thing you should notice is those little Li 1, Li 2, Li 3, etc, tabs right at the top. Each one can be turned on or off with that little check-box just below "Li 1" ... Each Lighting tab can be either global or positional, and you can change the colour of the light with the little button just below the on/off check-box.

Mandelbulb 3D Tutorial: The Basics

Alrighty! Finally decided to get down and start documenting all I've learnt so far about Mandelbulb 3D, a wonderful program for rendering 3D fractals.

Follow me on Tsu! Join up using this link: (It's invite-only, and you've just been invited =) ):
http://www.tsu.co/Mandelsage

First thing to say is, don't get intimidated by all the very technical math terms found when you open the program! You don't need to worry about most of it for now. (Though most of them, if you hover the mouse over them, will have a little description as to what they do in practical terms). Just follow my lead. So this is what the program looks like upon first opening it:

Also, two other windows open up with this one, called Formulas and Lighting, which I'll get to later.

The first thing I'm sure your eyes fixes upon is that big juicy looking button called "Calculate 3D" ... Go ahead and click on it ;D ... Here is what you should see after a quick rendering:

The True Cave of Lost Secrets, and A Dream of Death

I asked some of the guys at Fractal forums what they thought of why my Cave of Secrets image from the previous post looked so different from the original one on Daniel White's site, and Jesse, the creator of Mandelbulb 3D himself, gave me the answer: I was using the default Mandelbulb that loads when you open the program, but the original Cave of Secrets was rendered with a slightly different variation of the formula, known to me simply as the "CosinePow8" (found under the first "3D" tab in the formulas window.)

So I rendered it up, found the Cave, and tried to make it look exactly like the original. I'm zoomed a bit closer, the colouring is really not right, and somehow the original has more detail, but here is my result:

My version of the Cave of Lost Secrets by Daniel White. Click to enlarge.

The detail is really nothing like the original and I'm wondering -why- ? ... If someone knows of a setting to increase detail, please let me know. I've tried several things to no avail. But won't give up!

Next, my second attempt at 3D fractal art, "A Dream of Death" :

What do you all think? :) I'm very proud. Comments below will be greatly appreciated. I'll get to a "Mandelbulb 3D for beginners" Tutorial soon :) ... But right now, I'm really having fun just playing around.

Mandelbulb, 3D fractal maths, and me.

For the last few days, I've been trying to understand the mathematics behind the 3D Mandelbrot, the Mandelbulb. Apparently it works in exactly the same way as the 2D Mandelbrot, except where you had the "complex plane" before, upon which all points are mapped, you now have "hypercomplex space" ...

But unfortunately, I have yet to even begin to understand how it all works. Hell, I'm not even sure about how, in 2D fractals, i=sqrt(-1) ... This simply seems impossible to me, yet it all works when the maths is applied. I have a feeling that if I truly do want to understand such things, I would need to take a few steps back, go restudy the last few years of High School maths and then continue on to University level maths. But there's no way I can do that. The idea actually entices me because I've always loved mathematics and problem solving. So when it's combined with concepts like eternity and chaos, I REALLY get interested, but for now and for the foreseeable future, I just don't have the time.

But, for anyone who cares to try on their own, here's the Mandelbulb formula from Daniel White's site (One of the original discoverers of the 3D MAndelbulb). I tried using this as a starting point to further discover how it all worked, and failed:

What's the formula of this thing?

There are a few subtle variations, which mostly end up producing the same kind of incredible detail. Listed below is one version. Similar to the original 2D Mandelbrot, the 3D formula is defined by:

z -> z^n + c

...but where 'z' and 'c' are hypercomplex ('triplex') numbers, representing Cartesian x, y, and z coordinates. The exponentiation term can be defined by:

DeviantArt ID and fractal forums logo.

I woke up early this morning and, after shaking off the last of the unpleasantly weird dream I'd had, suddenly felt inspired. Didn't I still need to create a DeviantID ? Why yes, yes I did. So I got to it. I decided I wanted an image that would truly represent me, not only as an artist, but as a person.

So I got my camera, stood back, and silently said cheese. Then I sat down, opened photoshop and thought "Now what?" ... Well, I knew I was going to have to include something fractal in it, so I opened Fractal eXtreme and loaded good old Mandelbrot. It had to be Mandelbrot.

And to make a long story short, after some tinkering, this is now my deviantID:

So while I was feeling so creative, I decided to make a logo for fractalforums.com ... They allow their members to submit logos for random display every time you click a link.

Gostou? :) ...

Introduction to Fractals Tutorial

This tutorial consists of the following 4 pages (I highly recommend that you start from the first page and work your way through each, making sure you understand each one thoroughly before moving on to the next):

• Introduction
• Complex Numbers
• Julia sets, Functions and how Fractals are Generated
• The Mandelbrot Set

 

Fractal Art: A Start

So I've downloaded 4 different Fractal programs so far. Mandelbulb 3D and 3 different 2D applications: Fractal eXtreme, Xaos, and Ultra Fractal. Xaos I haven't really looked into much yet, played a bit with Ultra Fractal and as you all know, I've become quite familiar with Fractal eXtreme. Plus I tinkered around a little with Mandelbulb 3D :) Honestly, who could help it, after installing it?

Anyway, these are my results after trying to create something I would call "Art" ... Because really, though some extraordinarily beautiful images can be generated simply by zooming and choosing different formula sets, etc, one cannot really call that art. Art happens when you as a human being start consciously pursuing the image with a concept already in mind. (Though happy accidents sometimes happen, as is the case with one of the following pieces. I'll leave you to guess which :) ).

"Neuron of the God Emperor" ... Done in Fractal eXtreme

"Birth of a Blackhole" ... Done in Ultra Fractal

"The Crimson Army Evaded" ... Done with Mandelbulb 3D

So yes... You can't just randomly generate and zoom in to something that looks cool, save it, and call it art. This is not the Way. You might be able to fool some people, but never those of us who know, and most especially, never yourself. You'll soon lose interest, in fact, in doing empty, albethey aesthetically pleasing, pieces.

Personally, I've decided to go with conceptual themes whenever I'm looking to create something. I've come up with these three, that I'll use for now while I'm still in newbie phase:

Space (lol... couldn't have chosen an easier concept right?)

The Inner Mind

Creatures of the Dark vs. Creatures of the Light

...

Or something like that. Happy accidents might cause the birth and further exploration of alternate concepts. Art has no rules except the ones we create for ourselves ;)

Fractal eXtreme: The NovaM Set

I cannot begin to tell you how awesome this fractal set is... "The possibilities are infinite", as they say on Fractal Forums, and in the case of NovaM, this is truly the case. As with all the other sets I've shown you since the original Mandelbrot, I won't go into the maths of this one because honestly, even though I am more than capable of understanding it all if I wanted to, I'm just too fascinated with the colourful results to care. From what I remember from reading about it though, I can tell you that it is based on the Newton Set formula, but it adds a constant (either a real or complex number) after each iteration. This constant is what Fractal eXtreme allows you to vary, through the Plug-in Setup option.

And not only does it have that variable constant, it also has a Julia form... Are you starting to imagine what possibilities we have here? Well I'm gonna show you. First, take a look at the fascinating creature that loads as the NovaM default:

NovaM x: 3

Isn't it gorgeous? As the caption states, if you go have a look at its Plug-in Setup, you'll find x is 3, and y, 0.

From here, you have a multitude of options. You could simply start zooming in. Or, using Plug-in Setup, you could start changing that x value. (Or the y value, or both!) Just with this feature alone you can yield thousands of amazing Fractals to explore, yet it's only the beginning... For every change you make to those x and y values, you are able to generate an array of Julias and of course you're able to zoom into those as well(!).

Do you see how I spent hours playing with this Set last night?

Fractal eXtreme: The Hidden Mandelbrot Set

Ok, so here's one you can spend hours on, despite its rough, untidy appearance upon first loading:

Firstly, it isn't called the "Hidden Mandelbrot" for nothing. If you start zooming into the more interesting (less noisy) areas, you'll find you'll discover a few familar shapes :) (And yes, some that are not so familiar)... Have a look:

Really nice, right? :) Now, while there is no Plug-in Setup option for the Hidden Mandelbrot, you can generate Julias with it. Here are some good examples, with x/y locations:

Fractal eXtreme: The Auto Quadratic Set

This set is strange and unique. Upon first loading, you get this stretchy design:

 

Interesting, no? A swirly, stretchy monster. And indeed, if you're looking for any kind of swirling galaxy fractal, zooming into this Auto Quadratic is ideal, as these examples can attest:

But now, what other options are there? Julias? No, unfortunately not. But if you got to Options > Plug-in Setup you will find a "randomise" button. And when have you ever encountered a randomise button and not thought, Ooooh, I wonder what this does... And indeed, upon clicking on it, I discovered a myriad of different shapes and forms. In fact, I had a hard time forcing myself to stop clicking.

Fractal eXtreme: The Complex Newton Set

I'm excited about the next few posts because the fractals are getting really interesting and beautiful, and so much more fun to blog about. You'll now see a few perfect examples of why I got so into this fractal art thing in the first place. Also, after posting the next three (or so) posts, I'm going to really start making my own artistic pieces, as well as make some changes to this blog in order to showcase my future creations :)

But for this post, let me stick to the title: The Complex Newton Set. As you can see here, upon loading the default, it looks very similar to the Classic Newton:

The Complex Newton Set

But it has two more "spokes", and thus all the smaller self-similar iterations are different as well. Ok, cool, but now, what's nice about the Complex Newton is that you can change it's exponent. It can be either any real number (essentially, the shape cycles between having many more spokes to being a very slow-loading circle/eye-shaped thingy... ) or any complex number (much more interesting, as can be seen here):

Fractal Love

Just a quick post to demonstrate a small piece of creativity using fractals.

Yesterday was Dia dos Namorados (the Brazilian equivalent to Valentine's Day) and since I've become so enthralled with fractals recently, I thought why not try using them to create something special for the love of my life (Marianna)?

So using the Arbitrary Power Mandelbrot set, I found this beautiful design, and had it printed in photo quality for her. Happily, it came out so much better than I thought it would.

 

Then, now, I thought of something that I wish I had thought of on the actual day... Zooms of different spots in the above image, which I posted on Facebook, with the timeless words...:

 

All in all very happy with that :) ... Certainly more meaningful and less cheesy than a store-bought card.

Fractal eXtreme: The Barnsley Sets

In my previous post I said I would now go into all the other kinds of fractal sets Fractal eXtreme has available.  (Auto Quadratic, the "Hidden Mandelbrot", Barnsley 1, 2 and 3, Classic and Complex Newton, and Nova/NovaM).

I've since played around with those various sets and believe me, some of them are mind-blowing. The thing is, I can't fit them all in, in one post. So I'll start with the less interesting Barnsleys. Actually, before I start with them, let me just cover one that really doesn't merit much attention: The Classic Newton. This is what it looks like when it loads:

Actually I think I changed the colours to make it a bit more exciting, hehe. And sure, it doesn't look so bad, you might say. But here's the thing: When you zoom in, there's only more of the same. Truly, what you see above you is all there is. I got hopeful when I noticed it had a "Duplicate as Julia" option (which you may have noticed some of the others don't have) but surprise!, no matter where you Alt-click on the original, the Julia looks exactly the same! And thus, these are the last few seconds I will spend on this "fractal". (Ok, just a few more to give it at least this small tribute: It is the first step towards the Complex Newton, a much more interesting cousin).

Ok, now for the Barnsleys! Once again, I'll start with the more boring option: Poor old Barnsley 2. Upon loading, this it what you get:

Fractal eXtreme: Creating different kinds of Mandelbrot Sets.

It's been a few days since my last post because honestly, after understanding the basics behind what generates a fractal, especially the Mandelbrot, the next inevitable step for me was to download as many different Fractal programs as I could and start experimenting :) ... It has been a virtual mushroom trip, to say the least.

For now though, let me stick to Fractal eXtreme. Such a nifty little program! So much more to it than one initially thinks... You've probably played around with it a bit yourself already but for the sake of being complete, I'll start at the beginning.


The first obvious thing is that you need to do is choose a Set when the program opens. It's default is the standard and much loved Mandelbrot set, but you can choose from many others.

Listed below the Mandelbrot are more Mandelbrots using different powers in their formulas. As it explains in the program, the higher the exponent, the more nodes the Mandelbrot has (always one less node than the power).

There's also an option called Mandelbrot Arbitrary Power, which is a lot of fun. You know that the normal Mandelbrot set has the function f(z)=z^2 + c behind it. Well, with the Arbitrary Set, you can set the exponent to any real number you want. The resulting fractals can be out of this world.

Then, just when you thought the Arbitrary Power was cool, along comes: The Mandelbrot Complex Power ... That's right: z^(some complex number) + c ... Instead of jading you to the adjectives 'incredible' and 'amazing', let me show you. Examples to follow of selected Mandelbrots of which I've spoken about so far.

Mandelbrot normal exponent changes :

Standard Mandelbrot Set

Mandelbrot^3 [ f(z)=z^3+c ]

Mandelbrot^8 [ f(z)=z^8 + c ]

Arbitrary Power changes:

Mandelbrot^3.5

Mandelbrot^2.5

Mandelbrot^1.7

Complex Power changes:

Mandelbrot^(8,1.73i)

Mandelbrot^(3.1,2.5i)

Mandelbrot^(2.08,0.36i)

One thing you'll notice with making changes to the exponent in these ways is that, the higher the exponent, the longer it takes for the program to render a good-looking image, especially the more you zoom in. But you don't need to zoom in very far to discover really beautiful fractals. Go ahead and try some of the different Mandelbrots, experiment with colours, etc. To change the Arbitrary and Complex powers once you've loaded the default, you need to go to Options > Plug-in Setup.

And there you have it :) Hope you're having fun :) ... Fractal eXtreme has a few other very interesting options for creating new Fractals (Auto Quadratic, the "Hidden Mandelbrot", Barnsley 1, 2 and 3, Classic and Complex Newton, and Nova/NovaM), but those I'll show you in the next post.

Fractal eXtreme: Exploring the Mandelbrot set and Changing Colours

Ok, from here on out, I'm going to keep the maths down to a minimum :)

For the past few days, I've been playing around with Fractal eXtreme, often getting lost for hours within its beautiful depths. Now it's time to share with you all that I've learnt about it and the Mandelbrot set.

First, for all who have landed on this post first, and don't wish to go back and read all the maths explanations, here's what the Mandelbrot set looks like in Fractal eXtreme:

Really beautiful colour variations, no? And it's very easy to play around with the colours: Just go to Options > Colour Mapping, or Colour Palette.



Colour Mapping is for big, general changes. You'll see that changing the 'offset' is most effective, and adjusting the 'speed' can make things very interesting within a certain range.

The Mandelbrot Set

The Mandelbrot Set

 Ok, on we go to the fractal design that probably led you here in the first place... The famous Mandelbrot set.

So you know now that there are as many Julia sets as there are complex numbers (an infinite amount), and each set is generated according to the results of iterating the function f(x) = x² + c ... So in other words, for each and every Julia set, there is a corresponding formula, each having a unique value of c (either a real, imaginary, or complex number).

Did you play around with Fractal eXtreme as I suggested in the previous post? Really cool, right? But I bet you felt a bit restricted in terms of which numbers generated the coolest Julia sets. You may have noticed that entering anything under -2 in the X field didn't do anything too interesting. And the same for above 1. And in the Y field, you're were even more restricted. Anything above 1.4 or so, and under -1.4, hardly produced anything worth calling a fractal. This is because, as I explained in the previous post, Julia sets are coloured according to how fast all the points on their complex plane map out or "escape" to infinity. So when your c value (real,imaginary or complex number) is too big, obviously every point mapped with our function f(x) = x² + c escapes to infinity very very quickly, and thus, the image is coloured mostly monochromatic, (blue in the case of Fractal eXtreme's default colour scheme).

Ok, to continue... Take a look at these Julia set examples:

f(z)= z² + (0.3,0.01i)

f(z)= z² + (0.18,0.7i)

f(z)= z² + (-1.36,-0.05i)

f(z)= z² + (0.3,0.25i)

f(z)= z² + (-1.3,0i)

f(z)= z² + (-0.71,-0.17i)

Functions and Iterations, and how fractals are generated

To start, let me show you a few images of Julia set fractals.

 Beautiful, aren't they? But how on earth do we get to these amazing images, from the very simple-seeming mathematics previously described? Well, let's continue...

Ok, so in the previous post you learnt about what complex numbers are, and how to multiply them. But knowing this isn't really the most interesting thing in the world. What is interesting is what happens when you take any complex number and feed it into some function.